Introduction to Probabilistic Deep Learning

Why Bayesian deep learning?

Have you ever tried to learn about Bayesian neural networks but got hit in the face with a barrage of equations? Have you ever implemented a Bayesian neural network without actually understanding why this works?

If the answer is yes to any of those questions, then this blog is for you!
The goal of this series of posts is to provide a quick introduction to Bayesian neural networks. However, the focus of this blog would be “Why” rather than “How” and try to avoid any complicated concepts. With that in mind, let’s start our journey.

Introduction

University X decided to conduct a diabetes study, they recorded the age and blood glucose levels of 1,000 participants between the ages of 20 and 40.

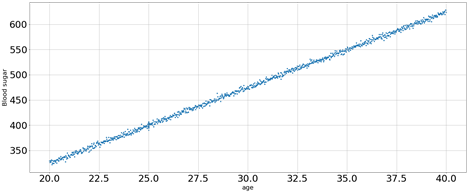
Then, they decided to build a model that, given the age, estimates the blood glucose level. Usually, when it comes to estimation, we can either estimate a single value, which is our best guess; these are called deterministic models. Or we can estimate a distribution of the different values of the blood glucose levels; these are called probabilistic models. The team needed the model to incorporate the uncertainty in the data in their study, so they decided to implement a probabilistic model.

The idea of the model is simple: given input x, a probability distribution of different values of y will be produced, instead of a single point. They also assumed that said distribution would be a normal distribution, now, they needed the model to produce a mean and a standard deviation given an input x.

So how exactly would we train such a model?
The basic concept is pretty straightforward, let’s take the participants at age 25 as an example. Normally, what we would want our model’s prediction to be as “close” as possible to the ground truths. In the case of probabilistic models, we would want our model’s prediction (in this case it’s a distribution rather than a single point) to fit the ground truths as best as we can. This is done using maximum likelihood. Below is an example of a distribution fit at x=25, now imagine a similar distribution fitted at each x, that would be the output of the probabilistic model.

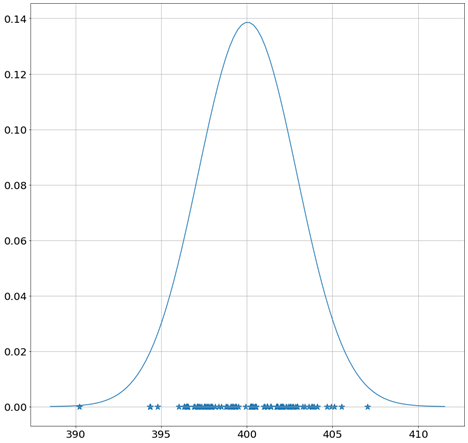
This approach works just fine until we get to x=35. There is only one observation, theoretically, you can use the same approach, however, there is a probability that this is not the right distribution.

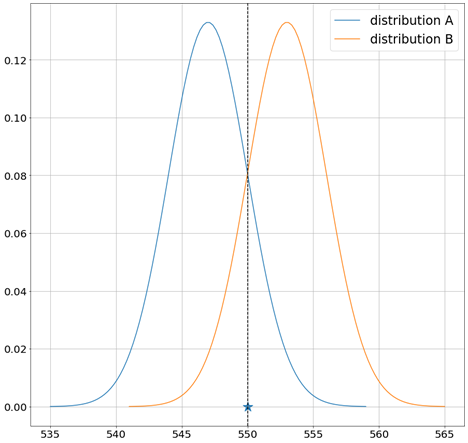
Both distributions A and B (seen in the figure above) have the same likelihood! This is the fall down of the maximum likelihood approach (also known as the frequentist approach).

So, to solve this problem, here’s an idea, how about considering EVERY possible distribution and taking a weighted average of them, where the weight is its likelihood, this way we can consider both distributions A and B, and every other possible distribution.
Does this idea make any sense to you? Yes? Congrats! This is essentially what Bayesian learning does!

Types of Uncertainty

In the previous example, we explained that uncertainty can be divided into 2 types.

Aleatoric Uncertainty

Aleatoric Uncertainty is the uncertainty we witnessed with the observations at age 25. It’s inherent uncertainty in data due to randomness, noise in measurement, error in measuring devices, etc. And no matter how much data you collect, you cannot reduce this uncertainty. This can be interpreted as the uncertainty in the value of y given x.

Epistemic Uncertainty

At x=35, we had a second type of uncertainty, we were uncertain of the distribution that describes the uncertainty in y. This is called epistemic Uncertainty and it exists in regions where there is observation sparsity or no data at all. Intuitively, collecting more data would decrease this uncertainty because the number of observations increases, and the number of distributions we consider decrease.
As we can see in the figure below, collecting another observation would make distribution B much more likely than A, hence decreasing the epistemic uncertainty.

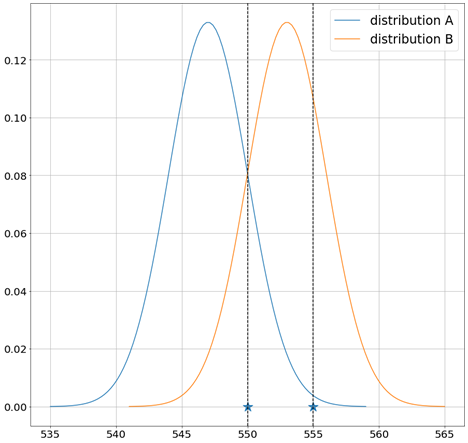
This type of uncertainty can be modeled using Bayesian learning, and this is why we need Bayesian neural networks!

Next blog, we will dig deeper into the idea of Bayesian learning.